There was for a long time a mathematical problem known as the knight's tour problem. It involved the moves of the knight pawn on a empty Chess board. The problem posed was to move the knight so that it visits every square (64) on the board – but only once. And, at the end of the tour it must come back to the square from which it began.
The first mathematician to investigate the Knight's tour problem was Leonhard Euler (1707 to 1783) , a Swiss mathematician. Since then it has come to be known as Euler Chess Knight Problem.
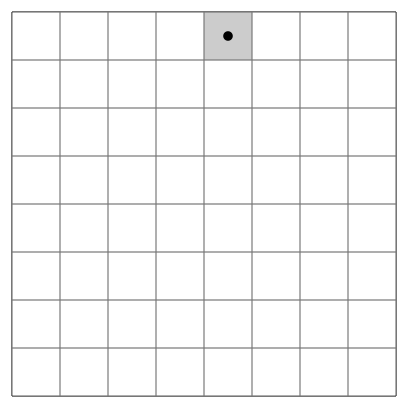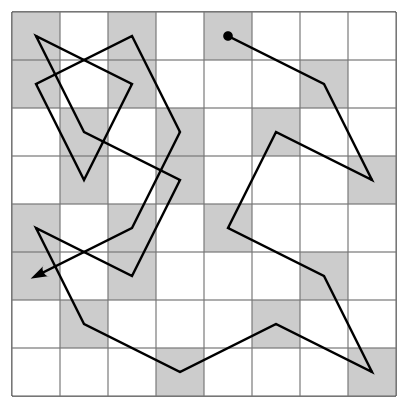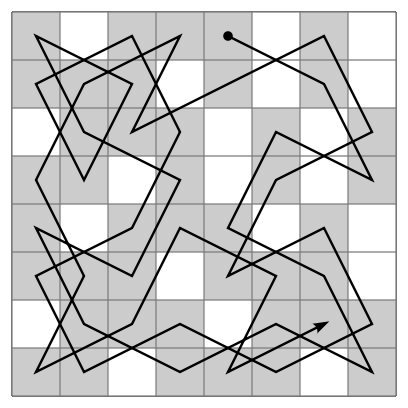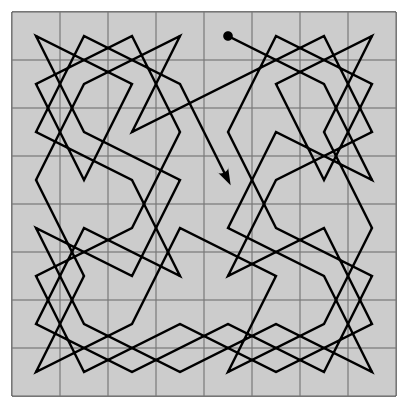
Sri Vedanta Desika (12-13th century) the remarkable scholar in his Paduka Sahasram celebrating the glory of Sri Ranganatha's padukas in 1008 verses employs Chitra-paddathi for 40 verses (911-950). Among these, the verse No.929 and N0.930 are hailed as astounding solution to the 'knight's tour problem'.
The syllables of the first Sloka (No.929) are posted, in sequence, on the squares of the Chess board.
O the sacred Padukas of the Brahman, you are adorned by those who have committed unpardonable sins; you remove all that is sorrowful and unwanted; you create a musical sound; (be pleased) and lead me to the feet of Lord Rangaraja.
Then if the syllables on the squares that the knight visits are put together in their sequence it produces the Sloka No.930
The Padukas which protect those who shine by their right attitude; who is the origin of the blissful rays which destroy the melancholy of the distressed; whose radiance brings peace to those who take refuge in them, which move everywhere, -may those golden and radiating Padukas of the Brahman lead me to the feet of Lord Rangaraja.
.The same table in English
| sthi 1 | rA 30 | ga 9 | sAm 20 | sa 3 | dhA 24 | rA 11 | dhyA 26 |
| vi 16 | ha 19 | thA 2 | ka 29 | tha 10 | thA 27 | ma 4 | thA 23 |
| sa 31 | thpA 8 | dhu 17 | kE 14 | sa 21 | rA 6 | sA 25 | mA 12 |
| ran 18 | ga 15 | rA 32 | ja 7 | pa 28 | dha 13 | mna 22 | ya 5 |
The second verse not only provided the solution to the knight's tour problem but went far beyond that. It is said composing such verse is far more difficult than solving the original Chess-knight problem. It is all the more amazing when you realize that Sri Vedanta Desika lived at least six hundred years before Euler.
Radhekrishna🙏 wonderful information. Dhanyosmi🙏💐✌👍
ReplyDelete